Polynomial Function

Another way that we can get values that aren’t just 1’s and 0’s is to model a function from points and get the speed of the robot from it – for example: let’s say that we start at speed 0.2, drive at full speed when we’re at half the distance and slow down to 0 when we’re at the end.

Polynomial function is a great candidate for this task. We can pick points that we want the function to pass through and then use polynomial regression to get the coefficients of the function.

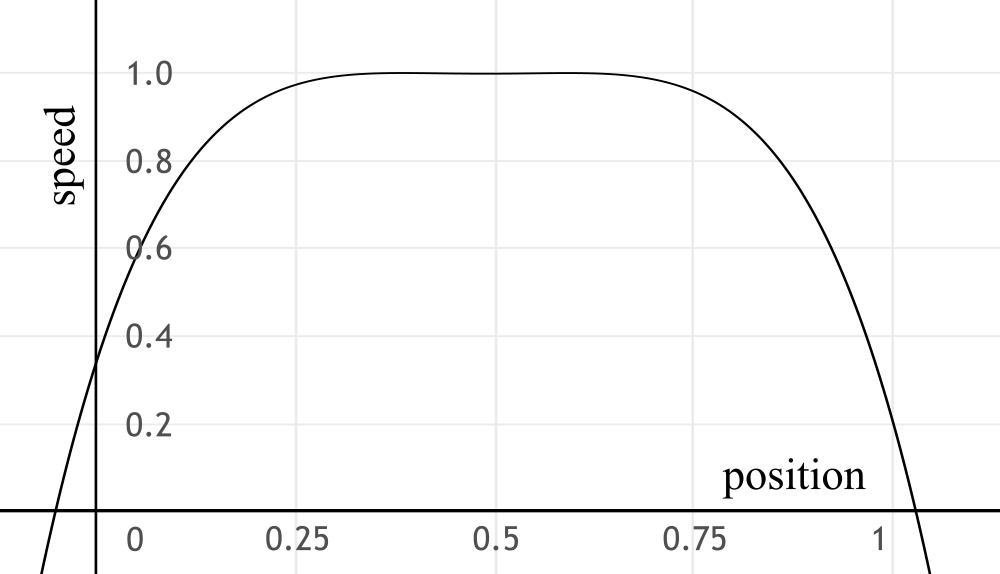
One thing you should also notice is that the function starts at \(x = 0\) and ends at \(x = 1\). This is deliberate – it makes it easy for us to “stretch” the function a little wider if we want to drive some other distance, not just a distance of 1.

Horner’s method

When it comes to programming, exponentiation tends to be quite expensive. Horner’s method is an elegant solution to this problem. The concept is simple – change the expression by repeatedly taking out \(x\), so there is no exponentiation.

This requires fewer multiplications, thus making the evaluation faster.

Implementation

The controller only needs the coefficients of the polynomial that we modeled, and a feedback function.

class PolynomialFunction:
    """A class implementing a polynomial function controller."""

    def __init__(self, coefficients, get_feedback_value):
        """Initialises the polynomial function controller from the polynomial
        coefficients and the feedback value."""
        self.coefficients = coefficients    # the coefficients of the function
        self.get_feedback_value = get_feedback_value   # the feedback function

    def get_value(self):
        """Returns the polynomial function value at feedback function value."""
        # calculate the x coordinate (by "stretching" the function by goal)
        x = self.get_feedback_value() / abs(self.goal)

        # calculate function value using Horner's method
        value = self.coefficients[0]
        for i in range(1, len(self.coefficients)):
            value = x * value + self.coefficients[i]

        # if the value is over 1, set it to 1
        if value > 1:
            value = 1

        # if goal is negative, function value is negative
        return value if self.goal > 0 else -value

    def set_goal(self, goal):
        """Sets the goal of the controller."""
        self.goal = goal

Examples

Driving a distance

Once again, the code is almost the exact same as the examples from nearly all of the other controllers.

# initialize objects that control robot components
left_motor = Motor(1)
right_motor = Motor(2)
encoder = Encoder()

# create a controller object and set its goal
controller = PolynomialFunction([-15.69, 30.56, -21.97, 6.91, 0.2], encoder)
controller.set_goal(10)

while True:
    # get the controller value
    controller_value = controller.get_value()

    # drive the robot using tank drive controlled by the controller value
    tank_drive(controller_value, controller_value, left_motor, right_motor)

Generating a polynomial

An alternative to “stretching” the polynomial to fit the goal is to specify the points the polynomial passes through and generate the coefficients after the goal is specified.

Say you have points \(\left(0,0.2\right)\), \(\left(0.4,1\right)\), \(\left(0.6,1\right)\) and \(\left(1,0\right)\). Since there are 4 points, the general form of the polynomial is \(y=ax^3+bx^2+cx+d\) Using this information, we can create a system of linear equations:

Solving this system of linear equations will give us the coefficients of the polynomial. We can apply this method to a polynomial of any degree \(d\), if we have at least \(d+1\) number of points.

Closing remarks

Although this controller isn’t as widely used as PID, it can sometimes outperform PID, namely in situations where the ranges of movement of the motors are restricted – forks of a forklift/robot arm.