Heading from Encoders

There are two things we need to know to approximate the position:

• Distance \(\Delta\) – how much did we move by?
• Heading \(\Delta\) – which way are we heading?

Assuming we have encoders on both sides of the robot, the distance is easy to calculate: we can read the values the encoders on both of the sides are reading and average them. Assuming we also have a gyro, heading is easy too: we can get the heading directly as the values the gyro is returning.

But what if we didn’t have a gyro?

Calculate heading without gyro

Although gyro is arguably the most precise way to measure the current heading, it’s not always available. It might be too expensive, impractical to include on a small robot, or not viable because of other conditions. In cases like these, it is good to know how to calculate heading only from the encoders.

Say the robot drove a small arc. The left encoder measured a distance \(l\) and the right side measured a distance \(r\). The length between the two wheels of the drivetrain is \(c\), the angle by which we turned is \(\omega\) (measured in radians), and \(x\) is just a variable to help with our calculations.

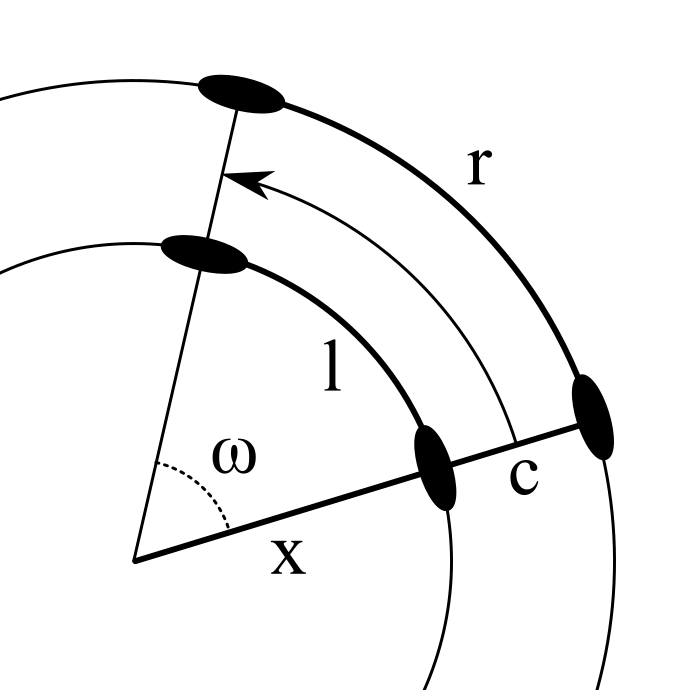
Let’s derive the equations for the lengths of the arches \(l\) and \(r\) in terms of the other variables (here is an article about arc length, if you need further clarification):

\[l=x\cdot\omega\qquad r=\left(c+x\right)\cdot\omega\]

We can then combine the equations, simplify, and solve for \(\omega\):

\[\frac{l}{\omega} = \frac{r}{\omega} - c\] \[\omega = \frac{r - l}{c}\]

And that’s it! The angle can be calculated from the difference of the readings of the encoders, divided by the length of the axis.