Line Approximation

For our first approximation, let’s make an assumption: instead of driving an arc, the robot will first turn by the specified angle, and only then drive the distance in a straight line.

This is quite a reasonable assumption to make for smaller angles: since we are updating the position multiple times per second, the angles aren’t going to be too large.

Line Approximation

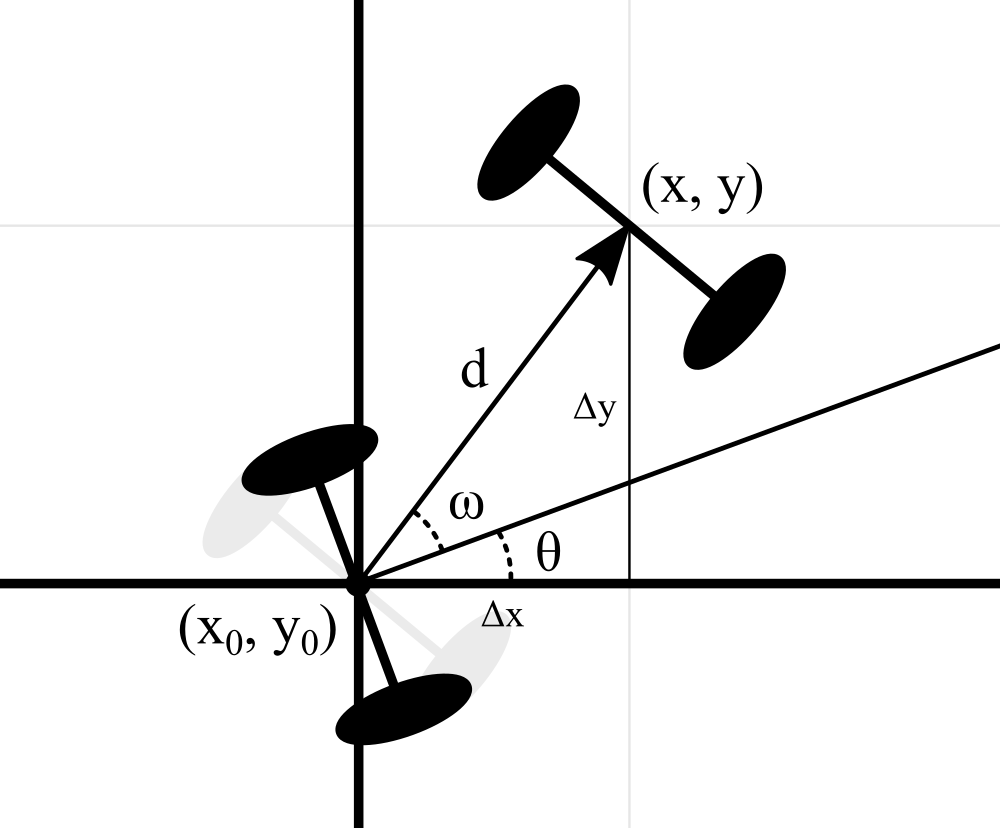
Deriving the equations

The robot moved a distance \(d\). It was previously at an angle \(\theta\) and is now at an angle \(\theta + \omega\). We want to calculate, what the new position of the robot is after this move.

One of the ways to do this is to imagine a right triangle with \(d\) being hypotenuse. We will use trigonometric formulas and solve for \(\Delta x\) and \(\Delta y\):

\[sin(\theta + \omega)=\frac{\Delta y}{d} \qquad cos(\theta + \omega)=\frac{\Delta x}{d}\] \[\Delta y = d \cdot sin(\theta + \omega) \qquad \Delta x = d \cdot cos(\theta + \omega)\]

The resulting coordinates \((x,y)\) are \(x=x_0+\Delta x\) and \(y=y_0+\Delta y\).

Implementation

This is one of the possible implementations of a class that tracks the current position of the robot by getting information from both encoders using the aforementioned line approximation method.

Note that for the position estimation to be accurate, the update() function of the class needs to be called multiple times per second.

from math import cos, sin


class LineApproximation:
    """A class to track the position of the robot in a system of coordinates
    using only encoders as feedback, using the line approximation method."""

    def __init__(self, axis_width, l_encoder, r_encoder):
        """Saves input values, initializes class variables."""
        self.axis_width = axis_width
        self.l_encoder,  self.r_encoder = l_encoder, r_encoder

        # previous values for the encoder position and heading
        self.prev_l, self.prev_r, self.prev_heading = 0, 0, 0

        # starting position of the robot
        self.x, self.y = 0, 0

    def update(self):
        """Update the position of the robot."""
        # get sensor values and the previous heading
        l, r, heading = self.l_encoder(), self.r_encoder(), self.prev_heading

        # calculate encoder deltas (differences from this and previous readings)
        l_delta, r_delta = l - self.prev_l, r - self.prev_r

        # calculate omega
        h_delta = (r_delta - l_delta) / self.axis_width

        # approximate the position using the line approximation method
        self.x += l_delta * cos(heading + h_delta)
        self.y += r_delta * sin(heading + h_delta)

        # set previous values to current values
        self.prev_l, self.prev_r, self.prev_heading = l, r, heading + h_delta

    def get_position(self):
        """Return the position of the robot."""
        return (self.x, self.y)